4 Simplicial homology
“Her thoughts were theorems, her words a problem,
As if she deem’d that mystery would ennoble ’em.”
— Lord Byron, in “Don Juan”
Simplicial complexes are excellent tools to model finite spaces.
4.1 What is a hole?
How can we detect a hole in a simplicial complex? Intuitively, a hole is something that is not there. In a circle, we have a boundary but have no “filling”.
Let’s reason using the following simplicial complex \(S\) (with vertex set \(V = \{a, b, c \}\) ) as an example:
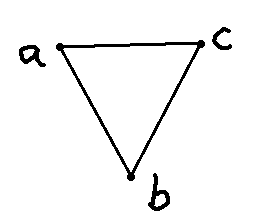
Let’s add a direction to the 1-simplices of \(S\) as follows:
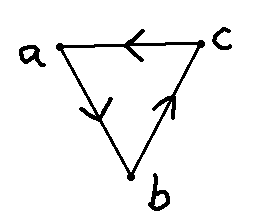
Intuitively, a 1-dimensional hole is formed when we have a sequence of 1-simplices \(a \to b \to c\) where the last element connect with the first, like a snake biting its own tail. It would be nice if we could detect these kind of cycles in a formal manner… Luckily for us, Poincaré was a very smart guy.
We will now try to define an algebra on \(S\) that allows us to detect cycles and holes.
To describe a segment in a vector space, we need only two points: the beggining \(u\) of the segment and its end \(v\). This vector can then be written as \(v-u\). Inspired by this, we define a function \(\delta\) called boundary operator on the edges of \(S\) by
\[ \delta([x, y]) = y - x. \]
But what is the meaning of \(a - b\)? This is just a “formal sum”: we treat \(a, b, c\) as a basis of a linear space. This vector space is called a free group on \(V\). We can also consider the same formal sums of 1-simplices, and extend \(\delta\) linearly, ie,
\[ \delta(e_1 + \lambda \cdot e_2) = \delta(e_1) + \lambda \cdot \delta(e_2) \]
for any \(e_1, e_2\) 1-simplices of \(S\). These vector spaces generated by the formal sums of \(S_k\) are denoted \(C_k(S)\) and called the simplicial k-chains, for k = 0, 1. We also impose that \([a, b] = -[b, a]\) (this is necessary to independ on the orientation).
Now, if we take the sum of the edges \([a, b], [b, c]\) and \([c, a]\), we have
\[ \delta([a, b] + [b, c] + [c, a]) = (b - a) + (c - b) + (c - a) = 0 \]
which means that a cycle has a trivial boundary. Define
\[ aaa \]
A hole is a boundary without it
homology as a tool to count holes; describe the algebra intuitively, formalise later