using MetricSpaces
using Images
using DataFrames
using GLMakie
using Ripserer, PersistenceDiagrams
import Plots
using ProgressMeter
using Clustering
import StatsPlots
using MultivariateStats
using Chain
using ImageFiltering5 Classifying wings
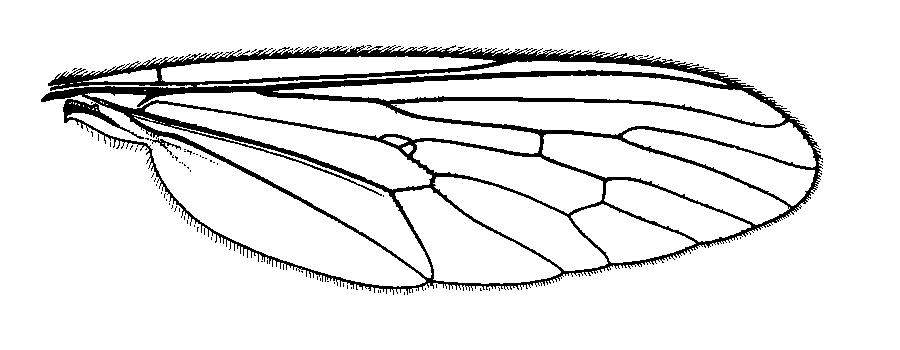
In this quick lesson, we try to classify wings using the tools seen in the last lessons.
We prepare a dataframe with the files and classes of each image
ds = DataFrame();
for (root, dir, files) in walkdir("wings/")
for file in files
dc = Dict(:Classe => root |> basename, :Caminho => file, :Caminho_completo => joinpath(root, file))
push!(ds, dc, cols = :union)
end
end
ds;ds_split = groupby(ds, :Classe) |> collect;function plot_mosaic(s)
mosaicview(
[imresize(load(f), (150, 300)) for f ∈ s.Caminho_completo[1:min(end, 21)]]
, ncol = 3
,fillvalue = RGB24(1)
)
end;
f = ds.Caminho_completo[1]"wings/Asilidae/Asilidae 11.png"5.1 The dataset
The dataset consists of several images of 3 different species of insects:
5.1.1 Asilidae
plot_mosaic(ds_split[1])5.1.2 Ceratopogonidae
plot_mosaic(ds_split[2])5.1.3 Tipulidae
plot_mosaic(ds_split[3])We load all images as matrices
images = [load(img) .|> Gray |> channelview for img ∈ ds.Caminho_completo];We can see that the image is indeed correct:
images[1] |> image
5.2 Matrix to \(\mathbb{R}^2\)
As before, we need to transform each image in points of the plane.
function img_to_points(img)
img2 = imfilter(img, Kernel.gaussian(1)) .|> float
ids = findall(x -> x <= 0.8, img2)
pts = getindex.(ids, [1 2])
[ [ p[1], p[2] ] for p in eachrow(pts)] |> EuclideanSpace
end;We convert each image to points
pts = img_to_points.(images);and normalize the coordinates, since each image has a different size:
function normalize!(pts)
a, b = extrema(pts .|> last)
pts ./ (b - a)
end
wings = normalize!.(pts);We can plot a scatter to check that it is indeed ok:
scatter(wings[1])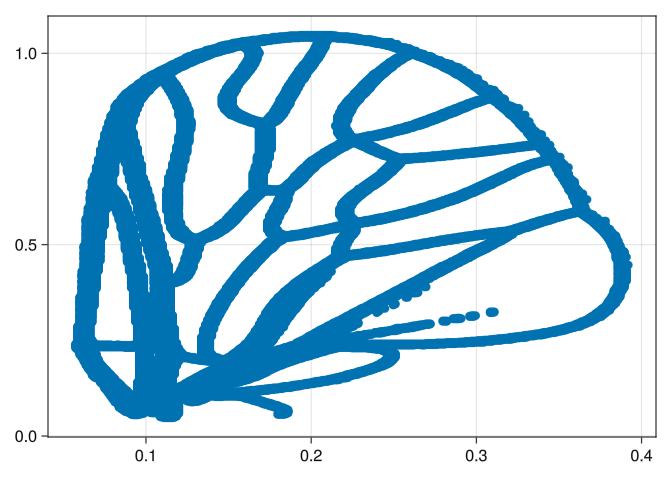
In order to apply the Vietoris-Rips filtration, we need to reduce the amount of points in each wing. The farthest point sample come in our rescue again!
wings_short = @showprogress map(wings) do w
ids = farthest_points_sample(w, 400)
w[ids]
end;Now we calculate each barcode using the Vietoris-Rips filtration:
pds = @showprogress map(wings_short) do w
ripserer(w, cutoff = 0.008)
end24-element Vector{Vector{PersistenceDiagram}}:
[400-element 0-dimensional PersistenceDiagram, 38-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 28-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 39-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 30-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 37-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 35-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 30-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 29-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 10-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 11-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 14-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 18-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 23-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 14-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 25-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 19-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 18-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 19-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 25-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 27-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 22-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 22-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 26-element 1-dimensional PersistenceDiagram]
[400-element 0-dimensional PersistenceDiagram, 23-element 1-dimensional PersistenceDiagram]We can now see the metric space
scatter(wings_short[1])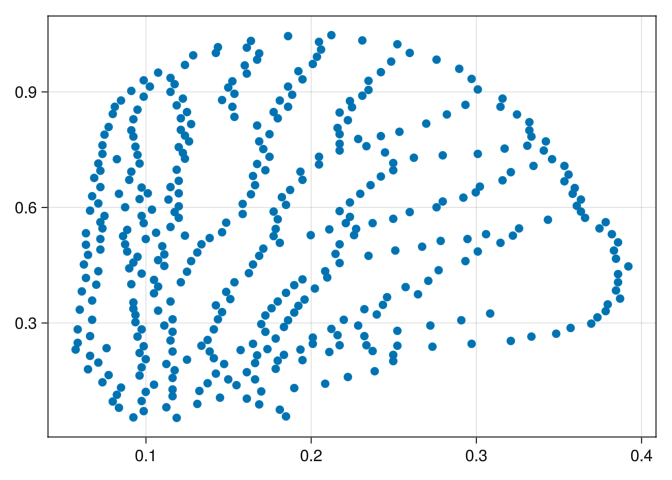
and the corresponding 1-dimensional persistente diagram
Plots.plot(pds[1][2])Now we calculate the pairwise 1-dimensional bottleneck distance between each wing:
function barcode_to_distance(pds)
n = length(pds)
DB = zeros(n, n)
@showprogress for i ∈ 1:n
for j ∈ i:n
if i == j
DB[i, j] = 0
continue
end
DB[i, j] = Bottleneck()(pds[i][2], pds[j][2])
DB[j, i] = DB[i, j]
end
end
DB
endbarcode_to_distance (generic function with 1 method)DB = barcode_to_distance(pds)24×24 Matrix{Float64}:
0.0 0.0158869 0.0135061 … 0.0462039 0.0469204 0.0283849
0.0158869 0.0 0.025868 0.0585658 0.0592823 0.0407468
0.0135061 0.025868 0.0 0.0326978 0.0334143 0.020432
0.00953908 0.0139792 0.0218124 0.0545102 0.0552267 0.0366912
0.0235501 0.035912 0.0142476 0.0226538 0.0233703 0.0116482
0.0230513 0.0182236 0.021989 … 0.0481824 0.0488989 0.0337146
0.0487406 0.0611025 0.0352345 0.0121581 0.0141773 0.0203557
0.014005 0.0263669 0.0123086 0.0321989 0.0329154 0.0143799
0.0245204 0.0388475 0.0299852 0.0494071 0.0501236 0.0338243
0.0341926 0.0285978 0.032716 0.0563412 0.05317 0.0411305
0.0189494 0.0260279 0.0276124 … 0.0603102 0.0610267 0.0424912
0.0276814 0.0249402 0.0411875 0.0738853 0.0746018 0.0560664
0.0305476 0.0283709 0.0314908 0.0641885 0.064905 0.0463696
0.02062 0.030228 0.023998 0.0552553 0.0559719 0.0374364
0.0250578 0.0200642 0.0235812 0.0472065 0.0440353 0.0343454
0.0683335 0.0559717 0.0818397 … 0.114537 0.115254 0.0967185
0.0334725 0.0458344 0.0204434 0.0127314 0.0134479 0.0178701
0.0211525 0.0335143 0.0116835 0.0284245 0.0312107 0.0190844
0.0288523 0.0412142 0.0153462 0.0173516 0.0180681 0.0145953
0.0518992 0.0642611 0.0383931 0.0139367 0.0114259 0.0235143
0.0395003 0.0518622 0.0259942 … 0.0153055 0.0159943 0.0122653
0.0462039 0.0585658 0.0326978 0.0 0.00844394 0.0213066
0.0469204 0.0592823 0.0334143 0.00844394 0.0 0.0185355
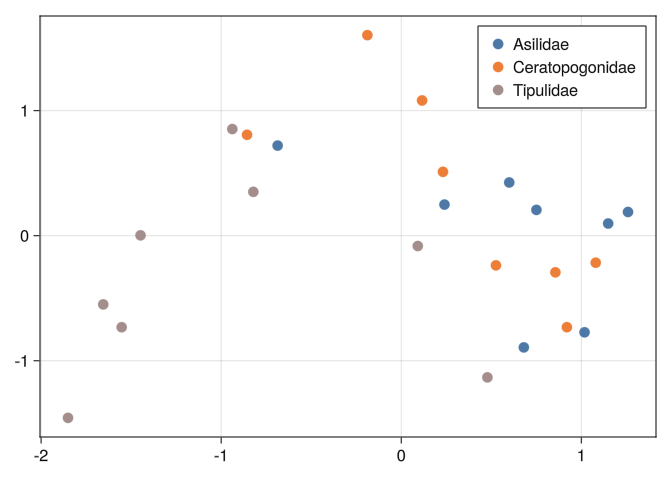
0.0283849 0.0407468 0.020432 0.0213066 0.0185355 0.0and see if the classes are well separated:
function mds_plot(D)
M = fit(MDS, D; distances = true, maxoutdim = 2)
Y = predict(M)
ds.Row = 1:nrow(ds)
dfs = @chain ds begin
groupby(:Classe)
collect
end
fig = Figure();
ax = Makie.Axis(fig[1,1])
colors = cgrad(:tableau_10, 8, categorical = true)
for (i, df) ∈ enumerate(dfs)
scatter!(
ax, Y[:, df.Row]
, label = df.Classe[1], markersize = 15
, color = colors[i]
)
end
axislegend();
fig
fig
end;mds_plot(DB)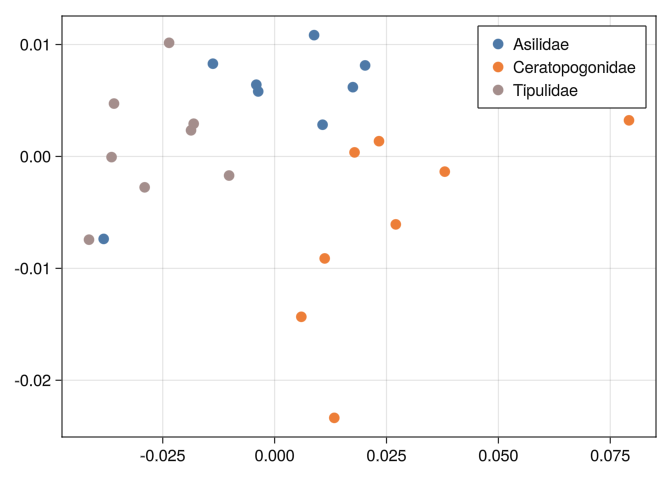
5.3 Slicing it sideways
As we did with the hand-written digits dataset, we can do some sideways slicing on the wings.
set_value(x, value) = x < 0.99 ? value : x
function side_filtration(img, axis = 1, invert = false)
img2 = imresize(img, (100, 200))
m = imfilter(img2, Kernel.gaussian(0.4))
# m = img .|> float
m = set_value.(m, 0)
# m |> image
# m = img .|> float
pts = img_to_points(m)
a, b = if axis == 1
extrema(pts .|> first)
else
extrema(pts .|> last)
end
for i ∈ a:b
v = (b - i) / (b - a)
if invert == true
v = 1.0 - v
end
if axis == 1
m[i, :] = set_value.(m[i, :], v)
else
m[:, i] = set_value.(m[:, i], v)
end
end
m .|> float
end;We can visualize the filtrations as follows:
img = images[5]
img2 = side_filtration(img, 1)
heatmap(img2)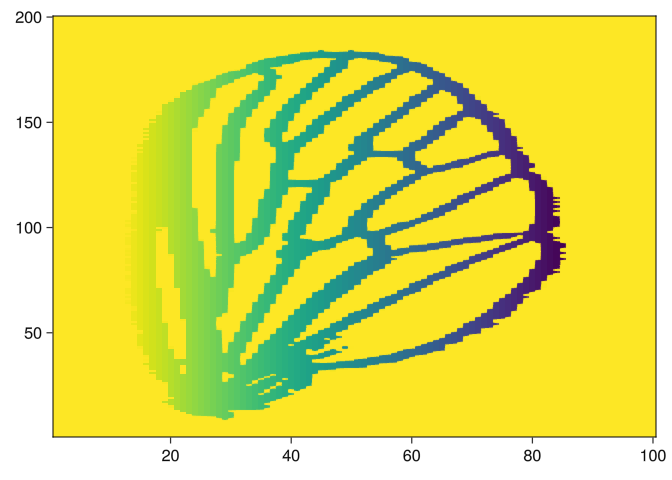
img2 = side_filtration(img, 2)
heatmap(img2)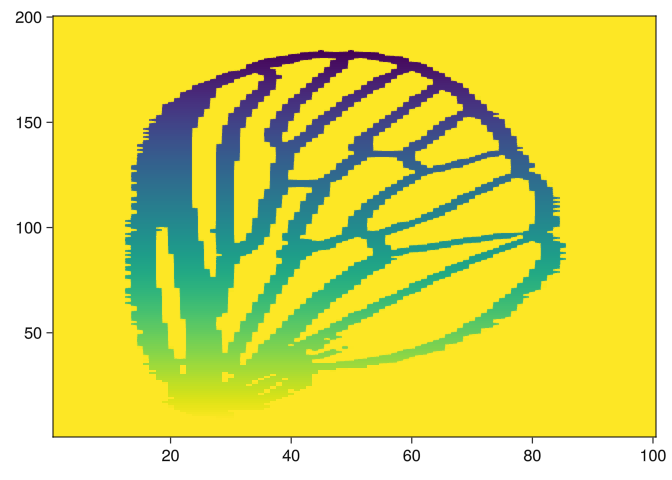
img2 = side_filtration(img, 1, true)
heatmap(img2)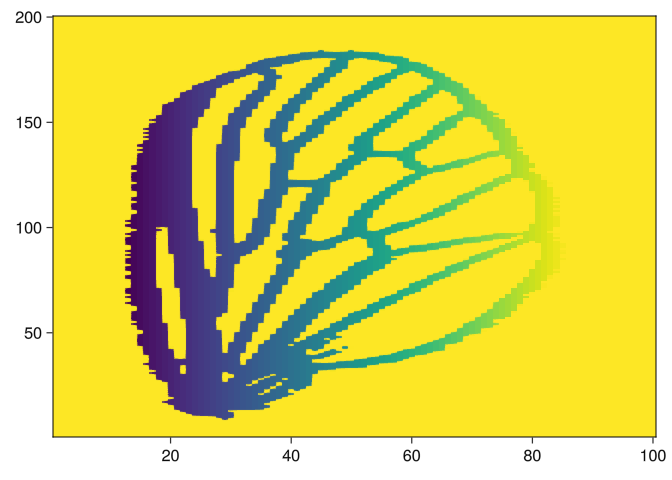
img2 = side_filtration(img, 2, true)
heatmap(img2)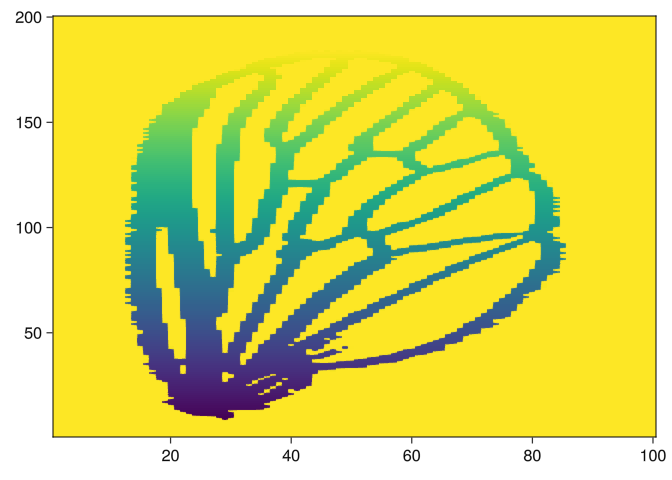
And calculate each barcode:
pds_x = @showprogress map(images) do img
img2 = side_filtration(img)
bc = ripserer(Cubical(img2), cutoff = 0.1)
end
pds_y = @showprogress map(images) do img
img2 = side_filtration(img, 2)
ripserer(Cubical(img2), cutoff = 0.1)
end
pds_x2 = @showprogress map(images) do img
img2 = side_filtration(img, 1, true)
ripserer(Cubical(img2), cutoff = 0.1)
end
pds_y2 = @showprogress map(images) do img
img2 = side_filtration(img, 2, true)
ripserer(Cubical(img2), cutoff = 0.1)
end24-element Vector{Vector{PersistenceDiagram}}:
[6-element 0-dimensional PersistenceDiagram, 17-element 1-dimensional PersistenceDiagram]
[3-element 0-dimensional PersistenceDiagram, 21-element 1-dimensional PersistenceDiagram]
[3-element 0-dimensional PersistenceDiagram, 13-element 1-dimensional PersistenceDiagram]
[2-element 0-dimensional PersistenceDiagram, 20-element 1-dimensional PersistenceDiagram]
[2-element 0-dimensional PersistenceDiagram, 16-element 1-dimensional PersistenceDiagram]
[4-element 0-dimensional PersistenceDiagram, 18-element 1-dimensional PersistenceDiagram]
[3-element 0-dimensional PersistenceDiagram, 21-element 1-dimensional PersistenceDiagram]
[5-element 0-dimensional PersistenceDiagram, 21-element 1-dimensional PersistenceDiagram]
[10-element 0-dimensional PersistenceDiagram, 40-element 1-dimensional PersistenceDiagram]
[4-element 0-dimensional PersistenceDiagram, 17-element 1-dimensional PersistenceDiagram]
[21-element 0-dimensional PersistenceDiagram, 18-element 1-dimensional PersistenceDiagram]
[7-element 0-dimensional PersistenceDiagram, 15-element 1-dimensional PersistenceDiagram]
[22-element 0-dimensional PersistenceDiagram, 21-element 1-dimensional PersistenceDiagram]
[39-element 0-dimensional PersistenceDiagram, 12-element 1-dimensional PersistenceDiagram]
[8-element 0-dimensional PersistenceDiagram, 15-element 1-dimensional PersistenceDiagram]
[19-element 0-dimensional PersistenceDiagram, 13-element 1-dimensional PersistenceDiagram]
[26-element 0-dimensional PersistenceDiagram, 10-element 1-dimensional PersistenceDiagram]
[36-element 0-dimensional PersistenceDiagram, 11-element 1-dimensional PersistenceDiagram]
[35-element 0-dimensional PersistenceDiagram, 6-element 1-dimensional PersistenceDiagram]
[23-element 0-dimensional PersistenceDiagram, 18-element 1-dimensional PersistenceDiagram]
[38-element 0-dimensional PersistenceDiagram, 14-element 1-dimensional PersistenceDiagram]
[29-element 0-dimensional PersistenceDiagram, 9-element 1-dimensional PersistenceDiagram]
[26-element 0-dimensional PersistenceDiagram, 5-element 1-dimensional PersistenceDiagram]
[17-element 0-dimensional PersistenceDiagram, 16-element 1-dimensional PersistenceDiagram]barcode(pds_x[5])barcode(pds_y[5])barcode(pds_x2[5])barcode(pds_y2[5])Let’s see way some figures have so many generators in dimension 1:
img = images[9]
img2 = side_filtration(img, 2, true)
heatmap(img2)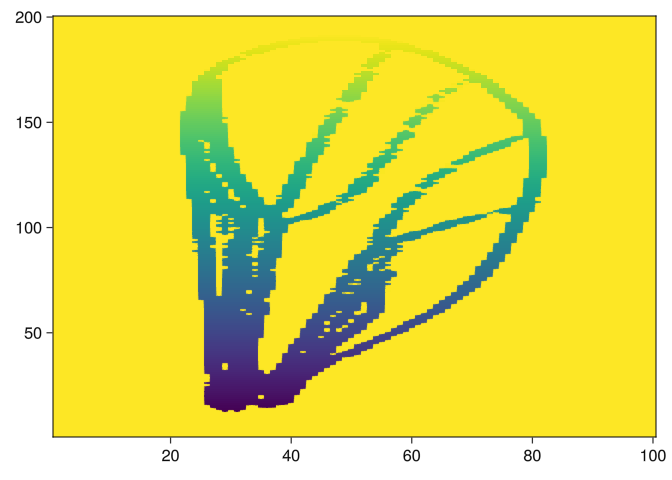
barcode(pds_y2[9])The respective distance matrices are obtained with
DB_x = barcode_to_distance(pds_x)
DB_y = barcode_to_distance(pds_y)
DB_x2 = barcode_to_distance(pds_x2)
DB_y2 = barcode_to_distance(pds_y2)24×24 Matrix{Float64}:
0.0 0.325713 0.298343 0.164898 … 0.502762 0.612723 0.289092
0.325713 0.0 0.380486 0.30512 0.599516 0.850059 0.316092
0.298343 0.380486 0.0 0.227273 0.472488 0.635195 0.289641
0.164898 0.30512 0.227273 0.0 0.465906 0.58974 0.278277
0.269424 0.324795 0.28 0.248831 0.523943 0.791427 0.282226
0.236258 0.381064 0.149272 0.133401 … 0.490336 0.653043 0.376954
0.337017 0.247476 0.491706 0.293634 0.552486 0.813468 0.364641
0.357143 0.214901 0.541667 0.326569 0.592159 0.773393 0.357143
0.630172 0.580911 0.675477 0.602126 0.734369 0.768504 0.640938
0.216896 0.497411 0.243819 0.196304 0.441745 0.735056 0.460388
0.30455 0.252874 0.535287 0.324666 … 0.612982 0.82798 0.340557
0.18034 0.333329 0.398941 0.252595 0.60662 0.704994 0.186046
0.386805 0.312664 0.62529 0.451256 0.800758 0.85196 0.436765
0.337017 0.482759 0.102273 0.232538 0.505535 0.610378 0.313947
0.243924 0.333329 0.468204 0.269936 0.699314 0.762496 0.188937
0.310581 0.362069 0.340765 0.289988 … 0.594937 0.835443 0.284884
0.414365 0.573856 0.448857 0.363636 0.463877 0.645959 0.589754
0.370159 0.482759 0.357955 0.329545 0.756637 0.873414 0.456036
0.558401 0.835113 0.573447 0.545455 0.484143 0.65033 0.79324
0.387342 0.317418 0.679487 0.491404 0.772375 0.820506 0.410405
0.318275 0.344828 0.25791 0.297683 … 0.633987 0.841502 0.238372
0.502762 0.599516 0.472488 0.465906 0.0 0.561036 0.744185
0.612723 0.850059 0.635195 0.58974 0.561036 0.0 0.804219
0.289092 0.316092 0.289641 0.278277 0.744185 0.804219 0.0And we can see that none of the tools we used before can separate well the classes:
mds_plot(DB)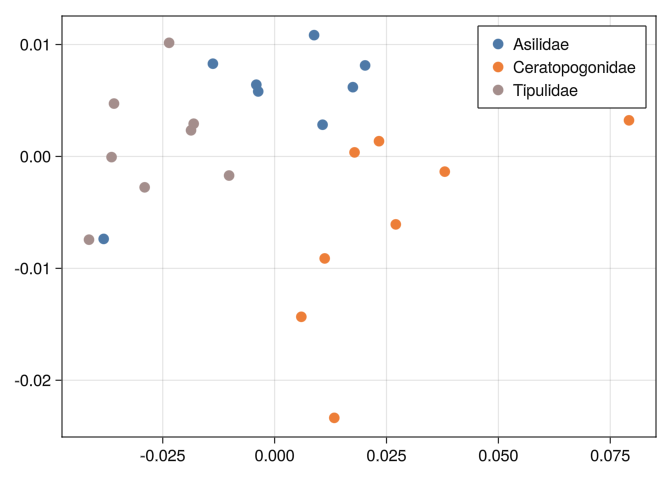
mds_plot(DB_x)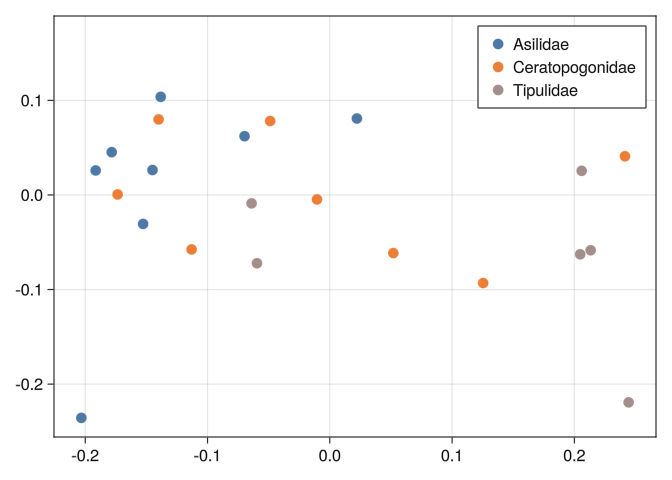
mds_plot(DB_y)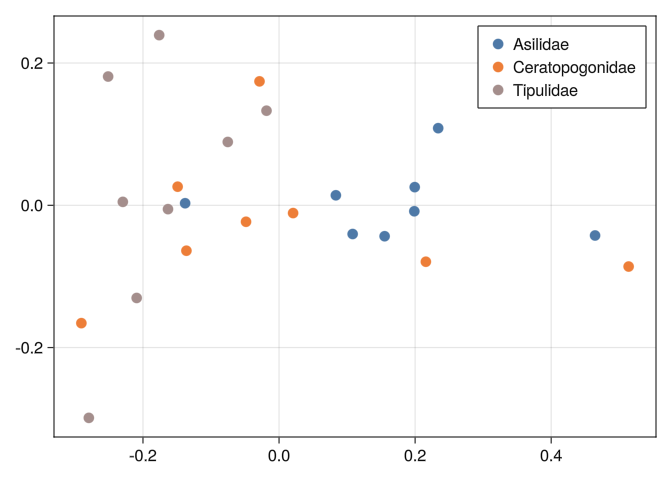
mds_plot(DB_x2)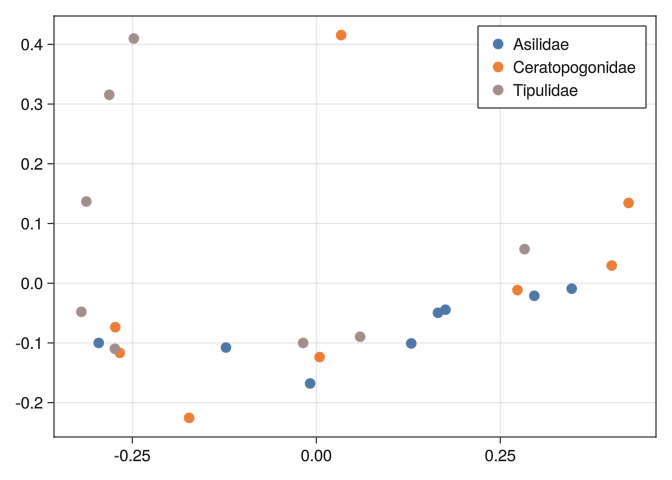
mds_plot(DB_y2)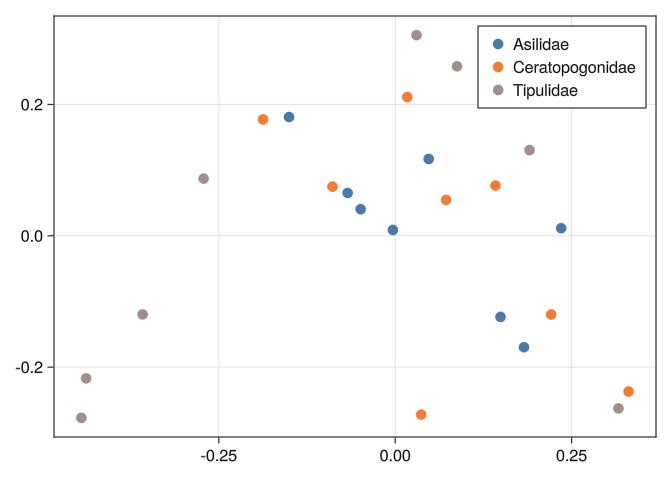
Even if we sum all these distances, we still can’t cluster correctly any class:
DB_final = zero(DB)
for d in [DB, DB_x, DB_y, DB_x2, DB_y2]
DB_final = DB_final + (d ./ maximum(d))
endmds_plot(DB_final)