import MLDatasets
using Images, Makie, CairoMakie
using Distances
using Ripserer, PersistenceDiagrams
using StatsBase: mean
import Plots;
using DataFrames, FreqTables, PrettyTables
using Flux, ProgressMeter4 Classifying hand-written digits
In this lesson, we will classify hand-written digits using the persistence homology and some tricks.
4.1 Loading packages
4.2 The dataset
MNIST is a dataset consisting of 70.000 hand-written digits. Each digit is a 28x28 grayscale image, that is: a 28x28 matrix of values from 0 to 1. To get this dataset, run
n_train = 10_000
mnist_digits, mnist_labels = MLDatasets.MNIST(split=:train)[:];
mnist_digits = mnist_digits[:, :, 1:n_train]
mnist_labels = mnist_labels[1:n_train];If the console asks you to download some data, just press y.
Notice that we only get the first n_train images so this notebook doesn’t take too much time to run. You can increase n_train to 60000 if you like to live dangerously and have enough RAM memory.
Next, we transpose the digits and save them in a vector
figs = [mnist_digits[:, :, i]' |> Matrix for i ∈ 1:size(mnist_digits)[3]];The first digit, for example, is the following matrix:
figs[1]28×28 Matrix{Float32}:
0.0 0.0 0.0 0.0 0.0 0.0 … 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 … 0.498039 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.25098 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 … 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
⋮ ⋮ ⋱ ⋮
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 … 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.215686 0.67451 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.533333 0.992157 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 … 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0We can see a mosaic with the first 10^2 digits
n = 10
figs_plot = [fig .|> Gray for fig in figs[1:n^2]]
mosaicview(figs_plot, nrow = n, rowmajor = true)4.3 A geometrical thinking
What topological tools can be useful to distinguish between different digits?
Persistence homology with Vietoris-Rips filtration won’t be of much help: all digits are connected, so the 0-persistence is useless; for the 1-dimensional persistence,
- 1, 3, 5, 7 do not contain holes;
- 2 and 4 sometimes contain one hole (depending on the way you write it);
- 0, 6, 9 contain one hole each;
- 8 contains two holes.
What if we starting chopping the digits with sublevels of some functions?
In Chapter 1 we talked about the Vietoris-Rips filtration to obtain a barcode. But there is also another useful way to create barcodes from data: sublevel filtrations.
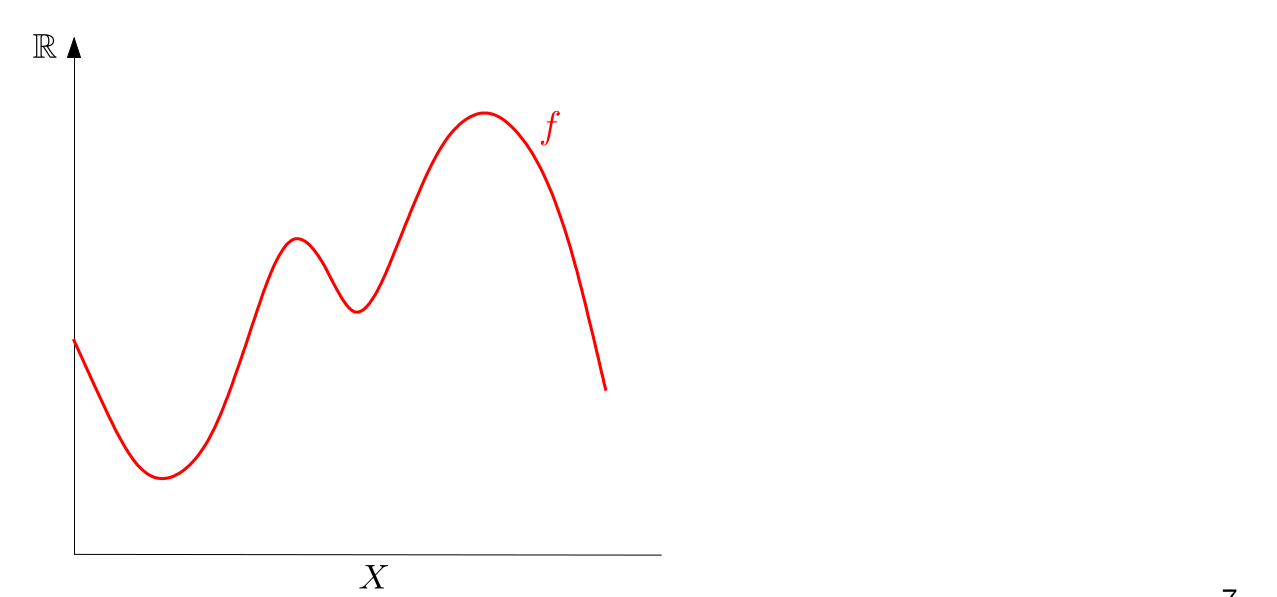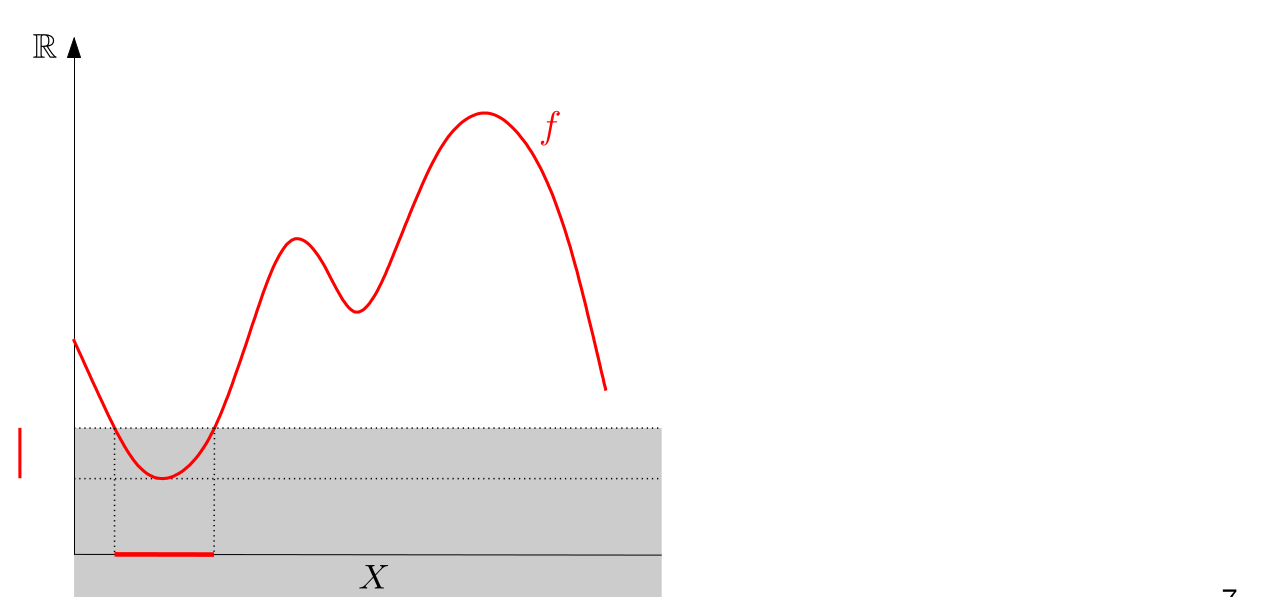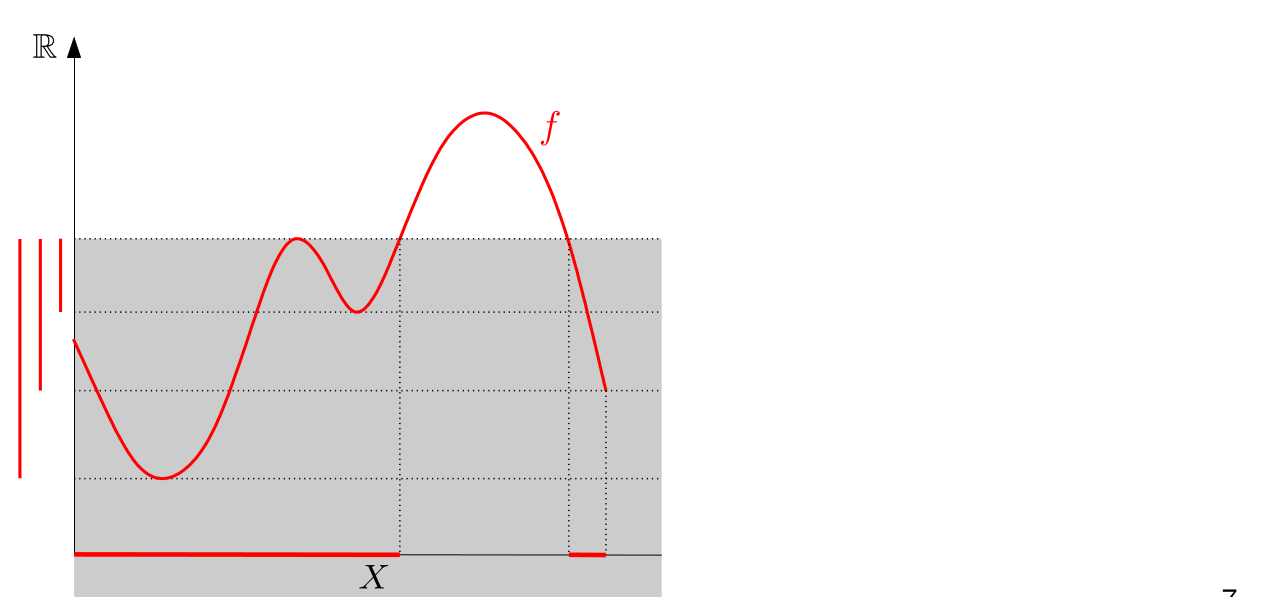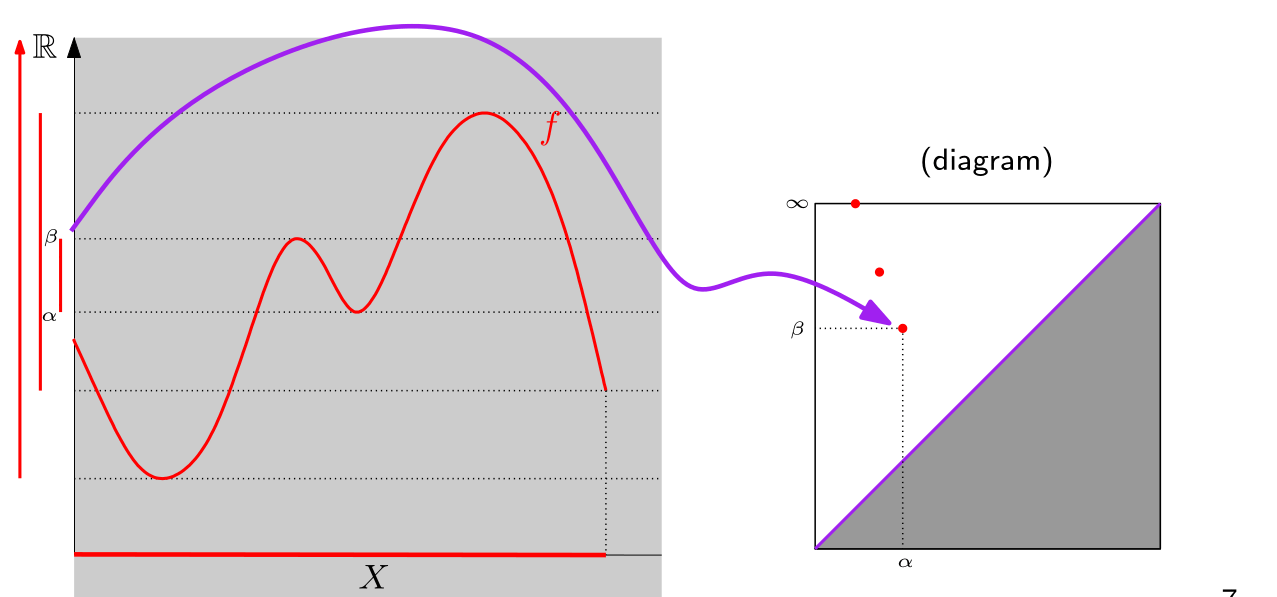
The excentricity function is able to highlight edges. Doing a sublevel filtration with the excentricity function will permit us to separate digits by the amount of edges they have. So 1 and 3 and 7, for example, will have different persistence diagrams.
4.3.1 From square matrices to points in the plane
In order to calculate the excentricity, we need to convert the “image digits” (28x28 matrices) to points in \(\mathbb{R}^2\) (matrices with 2 columns, one for each dimension, which we will call pointclouds). A simple function can do that:
function img_to_points(img, threshold = 0.3)
ids = findall(x -> x >= threshold, img)
pts = getindex.(ids, [1 2])
end;Notice that we had to define a threshold so we only get white pixels.
Let’s also define a function to plot a digit:
function plot_digit(fig, values = :black)
pt = img_to_points(fig)
f = Figure();
ax = Makie.Axis(f[1, 1], autolimitaspect = 1, yreversed = true)
scatter!(ax, pt[:, 2], pt[:, 1]; markersize = 40, marker = :rect, color = values)
if values isa Vector{<:Real}
Colorbar(f[1, 2])
end
f
end;We can see that it works as expected
fig = figs[3]
heatmap(fig)but the image is flipped. This is easily fixed:
heatmap(fig |> rotr90)4.3.2 Excentricity
The excentricity of a metric space \((X, d)\) is a measure of how far a point is from the “center”. It is defined as follows for each \(x \in X\):
\[ e(x) = \sum_{y \in X} \frac{d(x, y)}{N} \]
where \(N\) is the amount of points of \(X\).
Define a function that takes a digit in \(\mathbb{R}^2\) and return the excentricity as an 28x28 image
function excentricity(fig)
pt = img_to_points(fig)
dists = pairwise(Euclidean(), pt')
excentricity = [mean(c) for c ∈ eachcol(dists)]
exc_matrix = zeros(28, 28)
for (row, (i, j)) ∈ enumerate(eachrow(pt))
exc_matrix[i, j] = excentricity[row]
end
return exc_matrix
end;We store all the excentricities in the excs vector
excs = excentricity.(figs);and plot a digit with it’s corresponding excentricity
i = 5
fig = figs[i]
exc = excs[i]
heatmap(exc |> rotr90)Looks good! Time to chop it!
4.3.3 Persistence images
Now we calculate all the persistence diagrams using sublevel filtration. This can take some seconds. Julia is incredibly fast, but does not perform miracles (yet!).
pds = map(excs) do ex
m = maximum(ex)
ex = m .- ex
ripserer(Cubical(ex), cutoff = 0.5)
end;We check the first one
pd = pds[i]
pd |> barcodeCompare it with the corresponding heatmap above. There are 3 main edges (and one really small one). It seems ok!
We can see the “step-by-step” creation of these connected components in the following mosaic.
r = range(minimum(exc), maximum(exc), length = 25) |> reverse
figs_filtration = map(r) do v
replace(x -> x ≤ v ? 0 : 1, exc) .|> Gray
end
mosaicview(figs_filtration..., rowmajor = true, nrow = 5, npad = 20)Now we create the persistence images of all these barcodes in dimension 0 and 1. We pass the entire collection of barcodes to the PersistenceImage function, and it will ensure that all of them are comparable (ie. are on the same grid).
pds_0 = pds .|> first
pds_1 = pds .|> last
imgs_0 = PersistenceImage(pds_0; sigma = 1, size = 8)
imgs_1 = PersistenceImage(pds_1; sigma = 1, size = 8);The persistence images look ok too:
Plots.plot(
barcode(pds[i])
, Plots.plot(pds[i]; persistence = true)
, Plots.heatmap(imgs_0(pds[i][1]); aspect_ratio=1)
, Plots.heatmap(imgs_1(pds[i][2]); aspect_ratio=1)
, layout = (2, 2)
)Top left: the barcode of a digit with respect to sublevels using the excentricity function. Top right: the corresponding persistence diagram. Bottom: 0 and 1 dimensional persistence images. They create a pixelated view of the persistence diagram, using a gaussian blur.
4.4 Fitting a model
In order to use these persistence images in a machine learning model, we first need to vectorize them, ie, transform them into a vector. Machine learning models love vectors! The easist way is to just concatenate the persistence images as follows:
function concatenate_pds(imgs_0, pds_0, imgs_1, pds_1)
persims = [
[vec(imgs_0(pds_0[i])); vec(imgs_1(pds_1[i])) ] for i in 1:length(pds)
]
X = reduce(hcat, persims)'
X
end
X = concatenate_pds(imgs_0, pds_0, imgs_1, pds_1)
y = mnist_labels .|> string;We can see that X is a matrix with 10000 rows (the amount of digits) and 128 columns (the persistence images concatenated).
It was also important to convert the mnist_labels to strings, because we want to classify the digits (and not do a regression on them).
We now have a vector for each image. What can we do? We need a model that takes a large vector of numbers and try to predict the digit. Neural networks are excellent in finding non-linear relations on vectors. Let’s try one!
Create the layers
function nn_model(X)
model = Chain(
Dense(size(X)[2] => 64)
,Dense(64 => 10)
)
end
model = nn_model(X)Chain( Dense(128 => 64), # 8_256 parameters Dense(64 => 10), # 650 parameters ) # Total: 4 arrays, 8_906 parameters, 35.039 KiB.
the loader
target = Flux.onehotbatch(y, 0:9 .|> string)
loader = Flux.DataLoader((X' .|> Float32, target), batchsize=32, shuffle=true);the optimiser
optim = Flux.setup(Flux.Adam(0.01), model);and train it
@showprogress for epoch in 1:100
Flux.train!(model, loader, optim) do m, x, y
y_hat = m(x)
Flux.logitcrossentropy(y_hat, y)
end
end;The predictions can be made with
pred_y = model(X' .|> Float32)
pred_y = Flux.onecold(pred_y, 0:9 .|> string);And the accuracy
accuracy = sum(pred_y .== y) / length(y)
accuracy = round(accuracy * 100, digits = 2)
println("The accuracy on the train set was $accuracy %!")The accuracy on the train set was 70.79 %!Not bad, taking into account that we only used the excentricity sublevel filtration.
The confusion matrix is the following:
tbl = freqtable(y, pred_y)10×10 Named Matrix{Int64}
Dim1 ╲ Dim2 │ 0 1 2 3 4 5 6 7 8 9
────────────┼───────────────────────────────────────────────────────────
0 │ 920 0 21 16 2 6 13 2 13 8
1 │ 1 1078 7 11 4 5 0 21 0 0
2 │ 19 12 522 83 100 27 19 72 107 30
3 │ 6 36 37 757 18 52 7 100 13 6
4 │ 0 2 77 13 751 9 2 113 6 7
5 │ 13 40 46 310 11 283 14 118 6 22
6 │ 19 2 15 5 7 3 664 79 8 212
7 │ 2 41 35 49 126 20 42 753 2 0
8 │ 13 2 69 10 21 1 4 9 787 28
9 │ 13 1 29 17 14 6 219 102 13 564Calculating the proportion of prediction for each digit, we get
round2(x) = round(100*x, digits = 1)
function prop_table(y1, y2)
tbl = freqtable(y1, y2)
tbl_prop = prop(tbl, margins = 1) .|> round2
tbl_prop
end
tbl_p = prop_table(y, pred_y)10×10 Named Matrix{Float64}
Dim1 ╲ Dim2 │ 0 1 2 3 4 5 6 7 8 9
────────────┼───────────────────────────────────────────────────────────
0 │ 91.9 0.0 2.1 1.6 0.2 0.6 1.3 0.2 1.3 0.8
1 │ 0.1 95.7 0.6 1.0 0.4 0.4 0.0 1.9 0.0 0.0
2 │ 1.9 1.2 52.7 8.4 10.1 2.7 1.9 7.3 10.8 3.0
3 │ 0.6 3.5 3.6 73.4 1.7 5.0 0.7 9.7 1.3 0.6
4 │ 0.0 0.2 7.9 1.3 76.6 0.9 0.2 11.5 0.6 0.7
5 │ 1.5 4.6 5.3 35.9 1.3 32.8 1.6 13.7 0.7 2.5
6 │ 1.9 0.2 1.5 0.5 0.7 0.3 65.5 7.8 0.8 20.9
7 │ 0.2 3.8 3.3 4.6 11.8 1.9 3.9 70.4 0.2 0.0
8 │ 1.4 0.2 7.3 1.1 2.2 0.1 0.4 1.0 83.4 3.0
9 │ 1.3 0.1 3.0 1.7 1.4 0.6 22.4 10.4 1.3 57.7We see that the biggest errors are the following:
function top_errors(tbl_p)
df = DataFrame(
Digit = Integer[]
, Prediction = Integer[]
, Percentage = Float64[]
)
for i = eachindex(IndexCartesian(), tbl_p)
push!(df, (i[1]-1, i[2]-1, tbl_p[i]))
end
filter!(row -> row.Digit != row.Prediction, df)
sort!(df, :Percentage, rev = true)
df[1:10, :]
end
df_errors = top_errors(tbl_p)
df_errors |> pretty_table┌─────────┬────────────┬────────────┐
│ Digit │ Prediction │ Percentage │
│ Integer │ Integer │ Float64 │
├─────────┼────────────┼────────────┤
│ 5 │ 3 │ 35.9 │
│ 9 │ 6 │ 22.4 │
│ 6 │ 9 │ 20.9 │
│ 5 │ 7 │ 13.7 │
│ 7 │ 4 │ 11.8 │
│ 4 │ 7 │ 11.5 │
│ 2 │ 8 │ 10.8 │
│ 9 │ 7 │ 10.4 │
│ 2 │ 4 │ 10.1 │
│ 3 │ 7 │ 9.7 │
└─────────┴────────────┴────────────┘4.4.1 The perils of isometric spaces
How to separate “6” and “9”? They are isometric! For some people, “2” and “5” are also isometric (just mirror on the x-axis). Functions that only “see” the metric1 (like the excentricity) will never be able to separate these digits. In digits, the position of the features is important, so let’s add more slicing filtrations to our arsenal.
To avoid writing all the above code-blocks again, we encapsulate the whole process into a function
function whole_process(
mnist_digits, mnist_labels, f
; imgs_0 = nothing, imgs_1 = nothing
, dim_max = 1, sigma = 1, size_persistence_image = 8
)
figs = [mnist_digits[:, :, i]' |> Matrix for i ∈ 1:size(mnist_digits)[3]]
excs = f.(figs);
pds = map(excs) do ex
m = maximum(ex)
ex = m .- ex
ripserer(Cubical(ex), cutoff = 0.5, dim_max = dim_max)
end;
pds_0 = pds .|> first
pds_1 = pds .|> last
if isnothing(imgs_0)
imgs_0 = PersistenceImage(pds_0; sigma = sigma, size = size_persistence_image)
end
if isnothing(imgs_1)
imgs_1 = PersistenceImage(pds_1; sigma = sigma, size = size_persistence_image)
end
persims = [
[vec(imgs_0(pds_0[i])); vec(imgs_1(pds_1[i])) ] for i in eachindex(pds)
]
X = reduce(hcat, persims)'
y = mnist_labels .|> string
return X, y, pds_0, pds_1, imgs_0, imgs_1
end;We now create the sideways filtrations: from the side and from above.
set_value(x, threshold = 0.5, value = 0) = x ≥ threshold ? value : 0
function filtration_sideways(fig; axis = 1, invert = false)
fig2 = copy(fig)
if axis == 2 fig2 = fig2' |> Matrix end
for i ∈ 1:28
if invert k = 29 - i else k = i end
fig2[i, :] .= set_value.(fig2[i, :], 0.5, k)
end
fig2
end;and calculate all 4 persistence diagrams. Warning: this can take a few seconds if you are using 60000 digits!
fs = [
x -> filtration_sideways(x, axis = 1, invert = false)
,x -> filtration_sideways(x, axis = 2, invert = false)
,x -> filtration_sideways(x, axis = 1, invert = true)
,x -> filtration_sideways(x, axis = 2, invert = true)
]
ret = @showprogress map(fs) do f
whole_process(
mnist_digits, mnist_labels, f
,size_persistence_image = 8
)
end;We concatenate all the vectors
X_list = ret .|> first
X_all = hcat(X, X_list...);and try again with a new model:
model = nn_model(X_all)
target = Flux.onehotbatch(y, 0:9 .|> string)
loader = Flux.DataLoader((X_all' .|> Float32, target), batchsize=64, shuffle=true);
optim = Flux.setup(Flux.Adam(0.01), model)
@showprogress for epoch in 1:50
Flux.train!(model, loader, optim) do m, x, y
y_hat = m(x)
Flux.logitcrossentropy(y_hat, y)
end
end;Now we have
pred_y = model(X_all' .|> Float32)
pred_y = Flux.onecold(pred_y, 0:9 .|> string)
accuracy = sum(pred_y .== y) / length(y)
accuracy = round(accuracy * 100, digits = 2)
println("The accuracy on the train set was $accuracy %!")The accuracy on the train set was 95.15 %!which is certainly an improvement!
The proportional confusion matrix is
prop_table(y, pred_y)10×10 Named Matrix{Float64}
Dim1 ╲ Dim2 │ 0 1 2 3 4 5 6 7 8 9
────────────┼───────────────────────────────────────────────────────────
0 │ 99.6 0.0 0.1 0.0 0.1 0.1 0.1 0.0 0.0 0.0
1 │ 0.0 97.6 0.4 0.5 0.1 0.3 0.0 1.2 0.0 0.0
2 │ 0.0 1.3 82.2 1.8 0.1 9.3 0.5 4.6 0.0 0.1
3 │ 0.0 0.6 0.6 91.3 0.1 2.0 0.0 5.3 0.0 0.1
4 │ 0.0 0.2 0.0 0.0 98.4 0.0 0.3 0.5 0.1 0.5
5 │ 0.0 1.2 1.5 1.4 0.1 94.2 0.8 0.5 0.0 0.3
6 │ 0.0 0.2 0.2 0.0 0.1 0.5 98.9 0.1 0.0 0.0
7 │ 0.0 2.2 0.4 0.7 0.1 0.4 0.2 96.0 0.0 0.1
8 │ 0.0 0.2 0.7 0.1 1.1 0.3 0.1 0.3 95.0 2.1
9 │ 0.0 0.1 0.0 0.0 0.5 0.2 0.2 1.1 0.0 97.94.5 Learning from your mistakes
Let’s explore a bit where the model is making mistakes. Collect all the errors
errors = findall(pred_y .!= y);and plot the first 3
i = errors[1]
println("The model predicted a $(pred_y[i]) but it was a $(y[i])")
plot_digit(figs[i])The model predicted a 2 but it was a 1i = errors[2]
println("The model predicted a $(pred_y[i]) but it was a $(y[i])")
plot_digit(figs[i])The model predicted a 5 but it was a 2i = errors[3]
println("The model predicted a $(pred_y[i]) but it was a $(y[i])")
plot_digit(figs[i])The model predicted a 5 but it was a 2We can make a mosaic with the first 100 errors
n = 10
figs_plot = [figs[i] .|> Gray for i in errors[1:n^2]]
mosaicview(figs_plot, nrow = n, rowmajor = true)Many of these digits are really ugly! This makes them hard to classify with our sublevel filtrations. Some other functions could be explored.
4.6 Getting new data
Now we want to see if our model really learned something, or if it just repeated what he saw in the training data. To check data, we need to get new data and calculate the accuracy of the same model on this new data.
n_test = 5_000
new_mnist_digits, new_mnist_labels = MLDatasets.MNIST(split=:test)[:];
new_mnist_digits = new_mnist_digits[:, :, 1:n_test]
new_mnist_labels = new_mnist_labels[1:n_test];and obtaning X and y to feed the model
fs = [
x -> excentricity(x)
,x -> filtration_sideways(x, axis = 1, invert = false)
,x -> filtration_sideways(x, axis = 2, invert = false)
,x -> filtration_sideways(x, axis = 1, invert = true)
,x -> filtration_sideways(x, axis = 2, invert = true)
]
ret = @showprogress map(fs) do f
whole_process(
new_mnist_digits, new_mnist_labels, f
,size_persistence_image = 8
)
end;Define our new X and y
new_X = ret .|> first
new_X = hcat(new_X...)
new_y = ret[1][2]
new_pred_y = model(new_X' .|> Float32)
new_pred_y = Flux.onecold(new_pred_y, 0:9 .|> string);and calculate the accuracy:
accuracy = sum(new_pred_y .== new_y) / length(new_y)
accuracy = round(accuracy * 100, digits = 2)
println("The accuracy on the test data was $accuracy %!")The accuracy on the test data was 86.82 %!A bit less than the training set, but not so bad.
Let’s check the confusion matrix
tbl = prop_table(new_y, new_pred_y)10×10 Named Matrix{Float64}
Dim1 ╲ Dim2 │ 0 1 2 3 4 5 6 7 8 9
────────────┼───────────────────────────────────────────────────────────
0 │ 95.4 0.0 0.9 0.2 0.7 0.2 0.7 0.7 0.4 0.9
1 │ 0.2 96.3 0.9 0.4 0.4 0.4 0.2 1.4 0.0 0.0
2 │ 0.9 0.8 74.0 3.8 1.1 13.2 1.5 3.6 0.9 0.2
3 │ 0.2 1.2 4.6 79.0 0.0 5.4 0.2 8.8 0.4 0.2
4 │ 0.0 1.0 1.0 0.2 93.8 0.8 0.2 0.8 0.4 1.8
5 │ 0.4 1.5 9.4 4.4 1.5 79.2 0.4 1.5 1.1 0.4
6 │ 1.5 0.6 2.6 0.2 1.3 2.8 87.4 0.0 3.2 0.2
7 │ 0.2 3.3 2.1 2.1 4.9 1.4 0.0 85.4 0.0 0.6
8 │ 1.2 0.2 5.1 0.2 0.4 0.6 0.0 0.0 88.5 3.7
9 │ 0.2 0.8 0.6 0.0 4.0 0.6 0.4 2.9 1.9 88.74.7 Moral of the story
Even though we used heavy machinery from topology, at the end our persistence images were vectors that indicated the birth and death of connected components and holes. Apart from that, the only machine learning algorithm we used was a simple dense neural network to fit these vectors to the correct labels in a non-linear way.
State-of-art machine learning models on the MNIST dataset usually can get more than 99% of accuracy, but they use some complicated neural networks with many layers, and the output prediction are hard to explain. These methods, however, are not excludent of each other: we can use the persistence images (and any other vectorized output from TDA) together with other algorithms.
4.7.1 Exercise left to the reader
A curious reader can try to add more features to the input of the neural network, for example the amount of points, the mean excentricity, the and so on. Addin more features can improve the accuracy of the neural network.
If you are brave enough and want to get in the world of deep learning, a good exercise is to create a neural network with two parallel inputs - one for the digits images, followed by convolutional layers - other for the vector of persistence images, followed by dense layers can achieve a better result than the convolutional alone.
ie. are invariant under isometries↩︎